分散とは何か
分散とは、データの平均値から見た「ばらつき具合」を数値で表したもので、数学などでは統計学や確率論にて用いられる手法の1つとなります。
その数値の求め方は、
①各データの平均値との差を求める
②その差をそれぞれ2乗する
③全ての求めた数値を足す
④最後にデータの数で割る
以上となりますが・・・
「分散」という言葉自体を聞いたことのない方にとっては、何を言っているのか、非常に難しい説明と感じることでしょう。
わかりづらいと感じた方は、次のように覚えてください。
「計算された数値が、小さいほどデータのばらつきが少ない」
という意味で、つまり、出てきた数値が「0」に近いほどばらつきの無いデータということが分かる手法になります。
分散の求め方/VAR
実際に、その分散(ばらつき具合)を示す数値を求めるには、VAR関数を使用します。
=VAR(数値1, [数値2]・・・)
[数値1] = 分散を求める1つ目の数値、又は範囲を指定します。
[数値2] = 省略可。[数値1]の他に対象となる数値、又は範囲がある場合に指定します。
| 関数の説明 | 指定された数値の分散を求める関数 |
|---|---|
| EXCELバージョン | Excel2003 ・ Excel2007 ・ Excel2010 ・ Excel2013・ Excel2016 |
使い方例)VAR関数
下の表は、ある学校の学期末テスト結果を、クラス別に比べたものです。
それぞれ、平均点を求めた上で、点数のばらつき具合を求めることにしました。

① 「1-A」クラスの分散を求める。
(1)[数値] :セル範囲[C6:C11]を指定します。
=VAR(C6:C11)
② 「1-B」クラスの分散を求める。
(1)[数値] :セル範囲[F6:F11]を指定します。
=VAR(F6:F11)
以上で、分散の数値が求められます。
求めた数値の『読み方』(考え方)について・・・
分散の意味については、前述のとおりですが、今回の場合の「データの読み方」について見てみましょう。
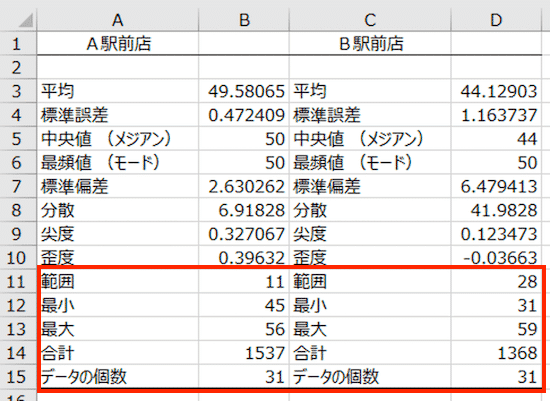
データの読み方①
まず、今回のデータでは、「1-B」クラスの方が平均点が高いのが分かります。
ですので、パッと見では当然『1-Bクラスの方が優秀である』と考えることが出来ます。
データの読み方②
では次に、分散値を見てみると、「1-A」クラスの方が小さい数値となっています。
この意味は、『1-Aクラスの方が平均した点数が取れている』という意味になります。
つまり、①と②から分かるのは、
[1-B]クラスは、高い点数が取れる優秀な生徒がいる一方で、点数のばらつきがあり、生徒間での学力の差が大きい。
[1-A]クラスは、飛びぬけて優秀な生徒がいるわけではないが、点数のばらつきが少なく、生徒間での学力の差は小さい。
という結果です。
教える側の先生としては、生徒の学力差を小さくするのも力量の見せ所となりますね。
分散の求め方/VARP
分散を求める関数として、VARP関数を使用しても問題ありません。
=VARP(数値1, [数値2]・・・)
[数値1] = 分散を求める1つ目の数値、又は範囲を指定します。
[数値2] = 省略可。[数値1]の他に対象となる数値、又は範囲がある場合に指定します。
| 関数の説明 | 指定された数値の分散を求める関数 |
|---|---|
| EXCELバージョン | Excel2003 ・ Excel2007 ・ Excel2010 ・ Excel2013・ Excel2016 |
使い方例)VARP関数
使い方は、VAR関数と全く同じですが、結果として表示される数値が若干違います。
① 「1-A」クラスの分散を求める。
(1)[数値] :セル範囲[C6:C11]を指定します。
=VARP(C6:C11)
② 「1-B」クラスの分散を求める。
(1)[数値] :セル範囲[F6:F11]を指定します。
=VARP(F6:F11)
VAR、VARPの違い
VAR関数も、VARP関数も使い方は同じなのに得られる結果が違うのは、それぞれ使用する時の条件が違っている為に起こるものです。
最初に、分散の計算方法として
①各データの平均値との差を求める
②その差をそれぞれ2乗する
③全ての求めた数値を足す
④最後にデータの数で割る
と説明しましたが、この④の部分に実は違いがあり、数値が違ってきます。
以下が、VAR関数とVARP関数の違いとなります。
VAR関数は・・・
指定したデータが、全体の内の「標本」(抜き出した一部分)として考え計算する関数。
全体のデータ数が不明の為、④の割り算は、「指定されたデータ数-1」で割るものし、得られる結果の偏りをなくします。
VARP関数は・・・
指定したデータが、「全て」の場合に使用する関数。
全体のデータ数=指定したデータとなる。
となります。
また、一般的に分散値を求める際には、「期待値」(=実際のばらつき具合に対する精度)が重要となり、例として以下のように考えられています。
- AクラスとBクラスでクラスの人数が違っていた場合、「指定されたデータ数-1」で割る分散値は、どちらのクラスにおいても期待値が等しくなるが、「指定されたデータ数のみ」で割る分散値は、人数が少ない組のほうが小さくなる傾向となる。
- Aクラスのうち、何人かが欠席して点数が未定の場合、「指定されたデータ数-1」で割る分散値は欠席にかかわらず期待値が等しくなるが、「指定されたデータ数のみ」で割る分散値は、欠席したほうが小さくなる傾向となる。
このため、数学の場では通常「分散」を求める際には、期待値のより正確な、VAR関数を使用されることが多いと言えます。
ここまで長く説明しましたが・・・・・・
やはり分かりづらいですね。つまりこう覚えておきましょう。
↓通常はこちらの関数を使用
「データが無限や非常に多い時、又はデータ数が一定でない場合はVAR関数」
「データが全て確定していて一定の場合はVARP関数」
図示例)VAR関数
VARとVARPの違いについては、人によってとても難解と感じる為、迷ったらVAR関数で一部分のデータを取り出して計算しましょう。